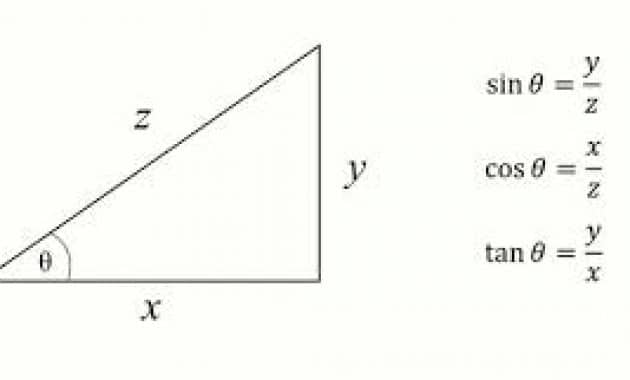
Rumus Sin Cos Tan – Sinus (sin), Cosinus (cos), Tangen (tan), Cotangen (cot), Secan (sec), dan Cosecan (cosec). Untuk informasi lebih lanjut tentang makna dan formula kalimat, lihat diskusi berikut.
Fungsi trigonometri dari sin cos dan tan sangat membantu ketika menghitung perhitungan sudut, terutama ketika menghitung sudut trigonometri dasar khusus.

Rumus Identitas Trigonometri
Identitas trigonometri adalah fitur unik yang hanya dapat ditetapkan untuk trigonometri, misalnya anomali air. Properti ini hanya miliknya. Dengan pengelompokan, tipe identitas ini dapat dibagi menjadi tiga kelas. Kelas pertama adalah identitas komparatif, kelas kedua adalah identitas terbalik dan yang terakhir adalah identitas Phytagore. Berikut adalah rumus trigonometri.
Baca Juga Rumus Volume Kubus
Tabel Sin Cos Tan
Di bawah ini adalah tabel cosco dengan semua sudut, yang disebut sebagai lingkaran penuh atau umumnya sebagai lingkaran 360º. Rumus sudut sin cos cos tan hingga 360 dalam tabel sangat berguna untuk menyederhanakan menjawab pertanyaan tentang rumus dan persamaan trigonometri, di mana garis sine cosinus tangen dibagi oleh 4 kuadran dalam sudut khusus trigonometri.
Relasi Sudut dalam Trigonometri
Dalam trigonometri ada hubungan antar sudut. Sudut dalam Kuadran II (90º-180º), Kuadran III (180º-270º) dan Kuadran IV (270º-360º) mengacu pada sudut dalam Kuadran I (0º-90º). Menurut rumus sudut terkait dalam trigonometri, berikut ini adalah trik untuk diingat.
Rumus Cepat Pola (lihat di kanan tanda =)
Sin → Sin
Cos → Cos
Tan → Tan
1. (180o – α) –> Kuadran II
sin (180o –
α) = sin α
cos (180o – α) = -cosα
tan (180o – α) = sin α
2. (180o + α) –> Kuadran III
sin (180o +
α) = -sin α
cos (180o + α) = -cosα
tan (180o + α) = sin α
3. (360o – α) –> Kuadran IV
sin (360o – α) = -sin α
cos (360o – α) = cosα
tan (360o – α) = -sin α
Baca Juga Rumus Volume Balok
4. (360o + α) –> Kuadran I
sin (360o +
α) = sin α
cos (360o + α) = cosα
tan (360o + α) = sin α
Pola (lihat di kanan tanda =)
Sin → Cos
Cos → Sin
Tan → Cot
5. untuk sudut (-α) –> Kuadran IV
sin (-α) =
-sin α
cos (-α) = cosα
tan (-α) = -sin α
6. (90o – α) –> Kuadran I
sin (90o –
α) = cos α
cos (90o – α) = sin α
tan (90o – α) = cot α
7. (90o + α) –> Kuadran II
sin (90o +
α) = cos α
cos (90o + α) = -sin α
tan (90o + α) = -cot α
8. (270o – α) –> Kuadran III
sin (270o –
α) = -cos α
cos (270o – α) = -sin α
tan (270o – α) = cot α
9. (270o + α) –> Kuadran IV
sin (270o +
α) = -cos α
cos (270o + α) = sin α
tan (270o + α) = -cot α
demikianlah artikel diatas dari ruangbimbel.co.id. smeoga artikel ini bermanfaat dan menambah wawasan kita semua. Terima kasih