Dalam kerangka matematika dan fisika, relevansi besaran turunan muncul sebagai kunci untuk membuka pintu pemahaman mendalam terhadap dinamika dunia di sekitar kita.
Artikel ini akan memperkenalkan relevansi besaran turunan, menyoroti peran esensialnya dalam berbagai bidang, mulai dari fisika dan matematika hingga aplikasi praktis dalam kehidupan sehari-hari.
Mari kita menjelajahi dunia yang terbentang di balik notasi matematika, di mana besaran turunan membawa makna dan relevansi yang mendalam.
Eksplorasi Besaran Turunan: Dalam Gaya Matematika dan Fisika
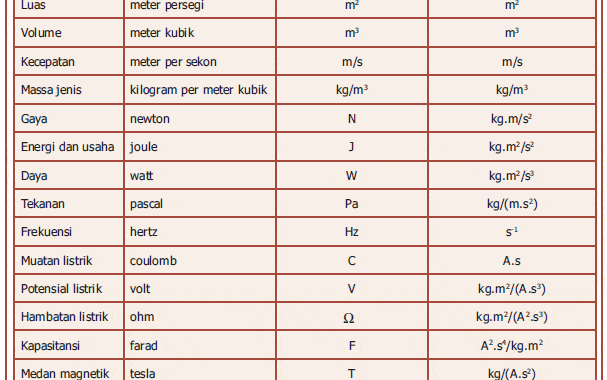
Besaran turunan merupakan konsep esensial dalam matematika dan fisika yang memungkinkan kita untuk memahami perubahan dan variasi di dalam berbagai fenomena.
Dalam artikel ini, kita akan menjelajahi makna, aplikasi, dan relevansi besaran turunan dalam konteks kedua disiplin ilmu tersebut.
Besaran turunan adalah konsep matematika yang berkaitan dengan perubahan suatu besaran terhadap variabel yang lain.
Dalam kalkulus, besaran turunan dinyatakan dengan deretan notasi matematis, seperti ( \frac{dy}{dx} ) yang menunjukkan turunan dari suatu fungsi (y) terhadap variabel (x).
Dalam kinematika, turunan waktu dari posisi sebuah objek memberikan kecepatan, dan turunan waktu dari kecepatan memberikan percepatan. Kedua besaran ini memungkinkan kita untuk memahami gerakan benda.
Turunan waktu dari momentum adalah gaya yang bekerja pada suatu objek. Konsep ini terkait erat dengan Hukum Newton yang menyatakan bahwa gaya adalah penyebab perubahan momentum.
Turunan waktu dari energi kinetik suatu objek memberikan daya, dan turunan waktu dari daya memberikan kerja. Ini adalah konsep penting dalam fisika energi dan pekerjaan.
Dalam kalkulus, kita dapat menghitung turunan fungsi matematika untuk menentukan kecepatan perubahan nilai fungsi terhadap variabelnya.
Turunan memberikan informasi tentang titik kritis dan nilai ekstrim fungsi, memungkinkan untuk optimisasi dan analisis grafik yang mendalam.
Besaran turunan muncul secara alami dalam persamaan diferensial, yang merupakan alat matematika untuk memodelkan dan memahami berbagai fenomena yang melibatkan perubahan.
Dalam ekonomi dan manajemen, analisis turunan membantu dalam pengambilan keputusan dengan menyediakan pemahaman tentang perubahan yang terjadi dalam suatu sistem.
Dengan meresapi konsep besaran turunan, kita dapat lebih mendalam memahami dinamika matematika dan fisika di sekitar kita.
Seiring dengan kemajuan teknologi dan penelitian, besaran turunan terus berperan penting dalam memecahkan teka-teki alam semesta dan membimbing perkembangan ilmu pengetahuan.
Memahami Posisi Bersama Turunan dalam Perjalanan Fisika: Mengungkap Gerak dan Dinamika
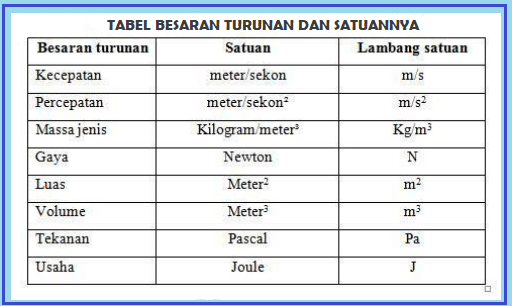
Dalam dunia fisika, posisi bersama turunan adalah konsep sentral yang memungkinkan kita untuk memahami dan memodelkan perjalanan suatu objek.
Artikel ini akan mengeksplorasi bagaimana konsep ini membentuk landasan bagi pemahaman gerak, kecepatan, dan percepatan dalam konteks fisika.
Posisi bersama turunan pertama, dikenal sebagai kecepatan, memainkan peran utama dalam melacak pergerakan objek.
Dalam istilah matematis, kecepatan ((v)) merupakan turunan pertama terhadap waktu dari posisi ((s)) suatu objek: (v = \frac{ds}{dt}).
Turunan kedua dari posisi adalah percepatan ((a)), yang mengukur perubahan kecepatan terhadap waktu: (a = \frac{dv}{dt} = \frac{d^2s}{dt^2}).
Percepatan memberikan informasi tentang seberapa cepat suatu objek mengubah kecepatannya, baik itu berupa peningkatan atau penurunan kecepatan.
Dalam konteks posisi bersama turunan, objek yang memiliki kecepatan tetap mengalami gerak beraturan, sedangkan objek yang mengalami perubahan kecepatan mengalami gerak berubah beraturan.
Dalam dunia nyata, posisi bersama turunan digunakan secara luas dalam dinamika kendaraan.
Kecepatan dan percepatan kendaraan menjadi kunci dalam desain jalur, keamanan berkendara, dan peningkatan efisiensi bahan bakar.
Selain kecepatan dan percepatan, konsep turunan lebih tinggi dari posisi seperti turunan ketiga dan seterusnya memberikan informasi tambahan tentang perubahan yang terjadi dalam gerakan suatu objek.
Konsep posisi bersama turunan tidak hanya relevan dalam pengajaran fisika sehari-hari, tetapi juga memiliki dampak besar dalam penelitian ilmiah.
Misalnya, analisis gerak planet dan benda langit lainnya di alam semesta mengandalkan prinsip-prinsip ini.
Dengan menggunakan konsep posisi bersama turunan, kita dapat membuat model matematika yang memprediksi perilaku objek dalam berbagai skenario. Ini membantu dalam perencanaan dan analisis eksperimen fisika.
Melalui pemahaman konsep posisi bersama turunan, fisikawan dapat mengurai kompleksitas pergerakan objek dan memahami aspek dinamika yang terlibat.
Dengan demikian, posisi bersama turunan membawa makna mendalam dalam mengungkap rahasia gerak dan dinamika alam semesta yang kita huni.
Relevansi Besaran Turunan: Mengungkap Signifikansi dalam Fisika dan Kehidupan Sehari-hari

Besaran turunan, meskipun mungkin terdengar abstrak, memiliki relevansi mendalam dalam banyak aspek fisika dan kehidupan sehari-hari.
Artikel ini akan menjelajahi relevansi besaran turunan, mengungkapkan bagaimana konsep matematika ini memainkan peran penting dalam memahami dan menggambarkan berbagai fenomena.
Besaran turunan pertama dari posisi, kecepatan ((v)), adalah konsep kritis dalam dinamika. Dalam konteks fisika, kecepatan membantu kita melacak pergerakan objek dan memahami sejauh mana suatu objek berubah posisi terhadap waktu.
Turunan kedua dari posisi memberikan kita percepatan ((a)). Percepatan menggambarkan laju perubahan kecepatan, yang merupakan faktor penting dalam pemahaman kekuatan dan gaya yang bekerja pada suatu objek.
Besaran turunan memainkan peran sentral dalam menganalisis berbagai jenis gerakan, termasuk gerak linier, gerak melingkar, dan gerak parabola.
Konsep ini membantu dalam merancang jalur, memprediksi posisi masa depan, dan memahami pola pergerakan.
Besaran turunan digunakan dalam konteks optimasi. Dalam dunia nyata, misalnya, untuk memaksimalkan keuntungan atau meminimalkan biaya, kita menggunakan konsep turunan untuk menemukan titik ekstrim dalam fungsi-fungsi tersebut.
Dalam ekonomi dan bisnis, besaran turunan terlibat dalam analisis harga, produksi, dan permintaan. Ini membantu perusahaan dan ekonom untuk membuat keputusan yang lebih baik dalam merespons perubahan pasar.
Dalam fisika makro, seperti gerakan planet dan benda-benda langit, besaran turunan memainkan peran kunci dalam menjelaskan fenomena alam.
Di tingkat mikro, seperti dalam mekanika kuantum, turunan memberikan wawasan tentang dinamika partikel subatom.
Melalui berbagai aspek ini, besaran turunan tidak hanya menjadi konsep matematika, tetapi juga alat analisis yang kuat dan serba guna dalam berbagai disiplin ilmu.
Relevansi besaran turunan ini menyiratkan bahwa pemahaman tentang besaran turunan bukan hanya berguna dalam konteks akademis, tetapi juga memberikan wawasan berharga untuk mengatasi tantangan dunia nyata.
Baca Juga: https://ruangbimbel.co.id/penerapan-fungsi-invers/