Pengertian barisan aritmatika sering digunakan untuk memodelkan pola pertumbuhan, baik itu dalam konteks matematika murni atau pada data dalam ilmu terapan.
Dalam pemodelan fisika dan teknik, barisan aritmatika dapat muncul dalam analisis pergerakan atau pertumbuhan suatu variabel dalam suatu sistem.
Ini membantu insinyur dan ilmuwan untuk merancang dan memahami fenomena fisika yang melibatkan perubahan teratur.
Memahami Langkah-Langkah yang Teratur: Inilah Barisan Aritmatika

Barisan aritmatika adalah serangkaian bilangan yang disusun secara berurutan dengan aturan penambahan atau pengurangan yang tetap antar setiap pasang suku berturut-turut.
Dengan kata lain, barisan ini memiliki pola pertambahan atau pengurangan yang konsisten, sehingga setiap suku dapat ditemukan dengan menambahkan atau mengurangkan nilai tetap dari suku sebelumnya.
Sebuah barisan aritmatika dapat diidentifikasi melalui dua elemen kunci: suku pertama ((a_1)) dan selisih antara dua suku berturut-turut ((d)).
Suku pertama memberikan nilai awal dalam barisan, sedangkan selisih ((d)) menunjukkan seberapa besar penambahan atau pengurangan antara setiap pasang suku.
Dengan informasi ini, kita dapat menentukan suku-suku berikutnya dalam barisan menggunakan rumus umum:
[ a_n = a_1 + (n-1)d ]
Di sini, (a_n) adalah suku ke-(n), (a_1) adalah suku pertama, (n) adalah urutan suku yang diinginkan, dan (d) adalah selisih antara suku-suku berturut-turut.
Contoh sederhana dari barisan aritmatika adalah 2, 5, 8, 11, 14, … dengan suku pertama ((a_1)) adalah 2 dan selisih ((d)) adalah 3. Dengan menggunakan rumus, kita dapat menghitung nilai suku ke-4 (n = 4):
[ a_4 = 2 + (4-1) \times 3 = 14 ]
Barisan aritmatika memiliki aplikasi luas dalam matematika dan ilmu terapan. Mereka digunakan untuk menganalisis pola pertumbuhan
Peramalan data, dan memecahkan masalah-masalah lain yang melibatkan urutan nilai dengan penambahan atau pengurangan tetap.
Dalam dunia nyata, barisan aritmatika dapat ditemui dalam pembayaran cicilan pinjaman, perhitungan pertumbuhan populasi, atau bahkan dalam mengatur barisan kursi di suatu tempat.
Pemahaman terhadap sifat-sifat barisan aritmatika menjadi dasar penting dalam pengembangan keterampilan matematika dan kemampuan analisis.
Sehingga, dengan merinci pengertian dan konsep di balik barisan aritmatika, kita dapat lebih mudah menggali kompleksitas serta menerapkan prinsip-prinsip matematika dalam berbagai konteks.
Menelusuri Jejak Reguler: Fungsi Barisan Aritmatika dalam Matematika dan Kehidupan Sehari-hari

Barisan aritmatika tidak hanya sekadar rangkaian angka yang bertambah atau berkurang dengan suatu selisih tetap, tetapi memiliki sejumlah fungsi penting
dalam matematika dan dapat memberikan wawasan yang berharga dalam berbagai aspek kehidupan. Berikut adalah beberapa fungsi barisan aritmatika:
Sebagai contoh, pertumbuhan ekonomi, populasi, atau penjualan dapat dimodelkan menggunakan konsep barisan aritmatika untuk mengidentifikasi tren dan pola kenaikan atau penurunan.
Dalam analisis statistik, barisan aritmatika digunakan untuk menyederhanakan data dan menyajikan informasi dengan cara yang lebih terstruktur.
Misalnya, peningkatan atau penurunan suatu parameter dari waktu ke waktu dapat diwakili oleh barisan aritmatika, memudahkan pemahaman tren.
Barisan aritmatika muncul dalam konteks perhitungan pembayaran tetap, seperti cicilan pinjaman atau pembayaran sewa.
Rumus barisan aritmatika digunakan untuk menghitung jumlah yang harus dibayar pada setiap periode, dengan suku pertama sebagai pembayaran awal dan selisih sebagai besaran cicilan tetap.
Barisan aritmatika merupakan kasus khusus dari progresi aritmatika, yang merupakan serangkaian bilangan yang bertambah atau berkurang dengan selisih tetap.
Progresi aritmatika dan barisan aritmatika memiliki peran utama dalam pembelajaran matematika diskrit dan pembuktian matematika.
Dalam bidang ilmu komputer, barisan aritmatika digunakan untuk merancang algoritma dan struktur data, terutama dalam pengalamatan memori.
Penerapan barisan aritmatika membantu mengorganisir dan mengelola alokasi memori dengan cara yang efisien.
Dengan fungsi-fungsi ini, barisan aritmatika bukan hanya alat matematika yang abstrak, tetapi juga alat analisis yang diterapkan dalam berbagai konteks kehidupan sehari-hari.
Pemahaman terhadap sifat-sifat barisan aritmatika membuka pintu untuk aplikasi luas dalam pemecahan masalah dan pengembangan berbagai bidang ilmu.
Manfaatkan sumber belajar yang tersedia, seperti buku pelajaran, video tutorial, atau materi online. Berbagai sumber dapat memberikan pendekatan yang berbeda dan memperkaya pemahaman Anda.
Memahami Secara Lebih Mudah: Tips Mempelajari Barisan Aritmatika
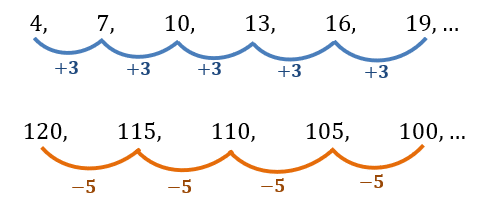
Mempelajari barisan aritmatika bisa menjadi tantangan, tetapi dengan pendekatan yang tepat, Anda dapat meraih pemahaman yang kokoh tentang konsep ini.
Berikut adalah beberapa tips yang dapat membantu Anda mempelajari barisan aritmatika dengan lebih mudah:
Mulailah dengan memahami konsep dasar barisan aritmatika. Pahami apa yang dimaksud dengan suku pertama ((a_1)), selisih ((d)), dan rumus umum (a_n = a_1 + (n-1)d).
Konsep ini adalah dasar dari pemahaman Anda terhadap barisan aritmatika. Mengidentifikasi pola ini membantu Anda memahami sifat dasar barisan aritmatika.
Terapkan konsep barisan aritmatika pada contoh-contoh nyata. Misalnya, jika Anda memahami bahwa setiap hari jumlah uang saku Anda bertambah 5 ribu rupiah, Anda telah memahami konsep barisan aritmatika.
Fokus pada pola pertambahan atau pengurangan yang tetap antar suku-suku dalam barisan. Apakah nilai suku selalu bertambah atau berkurang dengan jumlah yang sama?
Gunakan visualisasi untuk membantu pemahaman Anda. Gunakan diagram atau grafik untuk menggambarkan suku-suku dalam barisan. Ini membantu Anda melihat pola dan hubungan antar suku secara lebih jelas.
Ketika menggunakan rumus umum barisan aritmatika, pastikan Anda memahami setiap simbol. (a_n) adalah suku ke-(n), (a_1) adalah suku pertama, (n) adalah urutan suku, dan (d) adalah selisih antara suku-suku berturut-turut.
Berlatihlah dengan menyelesaikan berbagai jenis soal. Mulai dari soal yang sederhana hingga yang lebih kompleks.
Latihan membantu memperkuat pemahaman Anda dan meningkatkan keterampilan dalam menerapkan konsep barisan aritmatika.
Diskusikan konsep barisan aritmatika dengan teman atau bergabung dalam kelompok belajar.
Diskusi dengan orang lain dapat membuka sudut pandang baru dan membantu Anda mengatasi hambatan pemahaman.
Temukan aplikasi konsep barisan aritmatika dalam situasi sehari-hari. Hal ini membantu menjadikan konsep tersebut lebih nyata dan relevan dalam kehidupan Anda.
Dengan konsistensi, kesabaran, dan pendekatan yang sistematis, Anda dapat mempelajari barisan aritmatika dengan lebih mudah.
Teruslah melibatkan diri dalam latihan, dan ingatlah bahwa pemahaman bertahap akan tumbuh seiring waktu.
Baca Juga: https://ruangbimbel.co.id/teknik-dasar-permainan-bola-basket/